Нове дослідження виявило «абсолютну нестабільність» у моделі Сонячної системи

Вперше математики довели, що орбіти планет у Сонячній системі завжди залишатимуться нестабільними.

У 2009 році пара астрономів з Паризької обсерваторії повідомила про приголомшливе відкриття. Для нього вони створили складну комп’ютерну модель Сонячної системи та провели в ній кілька тисяч симуляцій, прогнозуючи рух планет на мільярди років уперед. У більшості цих симуляцій, в яких вихідна координата Меркурія варіювалася в діапазоні трохи менш як 1 метра, все йшло, як і очікувалося. Планети продовжували обертатися навколо Сонця, описуючи еліпсоподібні орбіти, які виглядали більш-менш так само, як і протягом всієї історії людства.

Але приблизно в 1 % випадків все йшло шкереберть – у буквальному сенсі. Форма орбіти Меркурія значно змінювалася. Його еліптична траєкторія поступово сплющувалася, аж поки планета або не падала на Сонце, або не зіштовхувалася з Венерою. Іноді, коли Меркурій торував свій новий маршрут у космосі, його рух дестабілізував й інші планети. Марс, наприклад, могло викинути з Сонячної системи, або він міг врізатися в Землю. Венера і Земля могли б у повільному космічному танці кілька разів обмінятися орбітами, перш ніж врешті-решт зіткнутися.

Можливо, Сонячна система не така стабільна, як людство вважало донедавна.

Минули століття, відколи Ісаак Ньютон сформулював свої закони руху і гравітації, відтоді математики й астрономи б’ються над одним і тим самим питанням. У найпростішій моделі Сонячної системи, яка враховує лише силу тяжіння Сонця, планети нескінченно довго рухаються по еліптичних орбітах, як у годинниковому механізмі. «Це досить втішна картина», – розповідає Річард Мокель, математик з Університету Міннесоти. «Цей рух триватиме вічно, і нас вже давно не буде, а Юпітер все ще обертатиметься навколо нашого світила».

Але як тільки до моделі додаються гравітаційне тяжіння між самими планетами, все стає набагато складніше. Більше не можна точно розрахувати положення і швидкості планет на довгі періоди часу, натомість доводиться вдаватися до аналізу якісних питань про те, як вони себе поведуть, зокрема чи можуть ефекти взаємного тяжіння впливати на рух планет.

Складні й кількісно підтверджені симуляції, такі як ті, що були опубліковані Жаком Ласкаром і Мікаелем Гастіно з Паризької обсерваторії у 2009 році, вказують на те, що існує невелика, але реальна ймовірність того, що все може вийти з-під контролю. Але ці симуляції, хоч і є важливими, не можуть слугувати математичним доказом. Вони не можуть бути абсолютно точними, і, як показують самі симуляції, невелика неточність може – протягом мільярдів імітованих років – призвести до дуже різних результатів. Крім того, вони не дають глибинного пояснення того, чому можуть розвиватися ті чи інші події. «Потрібно зрозуміти, які математичні механізми спричиняють нестабільність, і довести, що ці нестабільності насправді існують», – зазначає Марсель Гардія, математик з Університету Барселони. 

Тепер, у трьох статтях, загальний обсяг яких перевищує 150 сторінок, Гардія та двоє його колег вперше довели, що нестабільність неминуче виникатиме в моделі обертання планет навколо Сонця.«Результат дійсно вельми цікавий», – підтвердила Габріелла Пінзарі, професорка з фізики та математики з Університету Падуї, Італія. «Автори довели теорему, яка певно є однією з найкрасивіших теорем, які тільки можна довести». Можливо вона навіть допоможе пояснити, чому наша Сонячна система виглядає так, як вона виглядає.

Чотири сторінки та нова історія

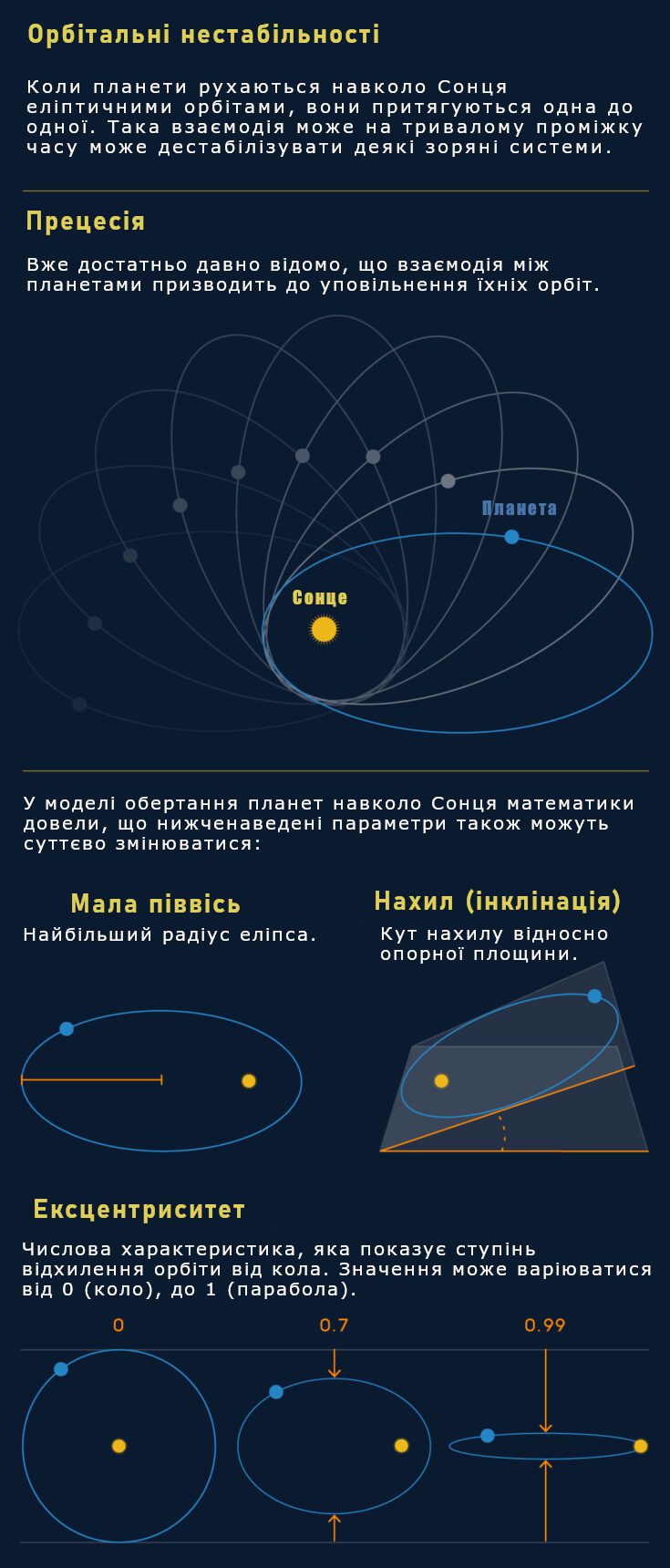
Вже кілька сторіч тому стало зрозуміло, що взаємодія між планетами може мати довгострокові наслідки. Візьмемо для прикладу Меркурій. Йому потрібно приблизно три місяці, щоб здійснити оберт навколо Сонця по еліптичній траєкторії. Але кут нахилу цього еліпса відносно центру мас, також повільно змінюється – на один градус кожні 600 років, тобто повний оберт кожні 200 000 років. Цей тип обертання, відомий як прецесія, здебільшого є результатом впливу Венери, Землі та Юпітера на Меркурій.

Але дослідження, проведені у 18 столітті такими геніями математики, як П’єр-Симон Лаплас і Жозеф-Луї Лагранж, показали, що, якщо не брати до уваги прецесію, розмір і форма еліпса залишаються стабільними. Лише наприкінці 19 століття ця теорія почала підлягатися критиці, коли Анрі Пуанкаре виявив, що навіть для моделі з трьома тілами (скажімо, зірка, навколо якої обертаються дві планети) неможливо обчислити точний розв’язок рівнянь Ньютона. «Небесна механіка – тонка річ, – стверджує Рафаель де ла Лаве, математик з Технологічного інституту Джорджії. Якщо змінити вихідні умови хоч трішечки – наприклад, змістивши передбачуване положення однієї планети всього на метр, як це зробили Ласкар і Гастіно у своїх симуляціях, – і на довгих часових відрізках система може набути зовсім іншого вигляду.

У задачі з трьома тілами Пуанкаре виявив настільки складний клубок можливих варіантів поведінки небесних тіл, що спершу вирішив, що зробив помилку. Як тільки він усвідомив істинність своїх результатів, вже неможливо було сприймати стабільність Сонячної системи як щось природне. Але оскільки працювати з рівняннями Ньютона дуже складно, залишалося незрозумілим, чи поведінка Сонячної системи буде заплутаною і хаотичною лише в малому масштабі – наприклад, планети можуть опинитися в різних положеннях в межах передбачуваного діапазону – або ж, як зрештою довели Гардія та його колеги у своїй моделі, розмір і форма орбіт можуть змінюватися настільки, що планети можуть зіткнутися одна з одною або відлетіти в нескінченність.

Тоді, у 1964 році, математик Володимир Арнольд написав статтю обсягом у чотири сторінки, яка сформулювала правильну постановку проблеми. Він знайшов конкретну причину, чому основні змінні в динамічній системі можуть так сильно змінюватися. Спочатку він створив штучний приклад – дивну суміш маятника і ротора, яка не нагадувала нічого з того, що можна зустріти в природі. На цій іграшковій моделі він довів, що за певний час певні величини, які зазвичай залишаються постійними, можуть сильно змінитися.

Арнольд припустив, що більшість динамічних систем повинні демонструвати подібну нестабільність. У випадку Сонячної системи це може означати, що форми орбіт або ексцентриситет певних планет може потенційно змінюватись протягом мільярдів років.Хоча математики й фізики з часом досягли значного прогресу в доведенні того, що виникнення нестабільності відбувається завжди, їм не вдалося продемонструвати це на прикладі моделей небесних тіл. Все тому, що гравітаційний ефект Сонця настільки сильний, що багато особливостей планетарної моделі, де тіла обертаються наче стрілки у годинниковому механізмі, зберігаються навіть тоді, коли ви враховуєте додаткові сили, що діють на планети. У цьому контексті ньютонівська механіка дає настільки гарне наближення до реальності, що ці моделі не потребують врахування ефектів загальної теорії відносності. Парадокс у тому, що така внутрішня стабільність ускладнює виявлення загальної нестабільності.Чи могли параметри, які залишалися такими стабільними в розрахунках Лапласа, Лагранжа та інших, насправді суттєво змінюватися? «Ви маєте справу з нестабільністю, яка є надзвичайно слабкою, – каже Лоран Нідерман з Університету Париж-Сакле. Звичними методами її не вловити.Цифрове моделювання давало надію на те, що полювання за доказами не було марним. Були й перші результати. У 2016 році, наприклад, де ла Лаве та двоє його колег довели існування нестабільності у спрощеній небесній моделі, що складалася з Сонця, планети та комети, де передбачалося, що комета не має маси, а отже, не чинить гравітаційного впливу на планету. Ця модель відома як «обмежена» проблема n-тіл.У нових роботах розглядається справжня проблема n-тіл – демонструється, що нестабільність виникає в планетній системі, де три малих тіла обертаються навколо набагато більшого Сонця. Попри те, що розмір і форма орбіт може тривалий час коливатися навколо постійних значень, врешті-решт вони кардинально зміняться.Цього можна було очікувати – широко поширена думка, що стабільність і нестабільність співіснують у такого роду моделях, – але герої цієї статті стали першими математиками, які це довели.

Абсолютна нестабільність

Гардія разом з Жаком Фежосом з Університету Париж IX вперше спробував довести існування нестабільності в задачі трьох тіл (одне сонце, дві планети) у 2016 році. Хоча вони змогли встановити, що хаотична динаміка виникла в стилі розрахунків Пуанкаре, вони не змогли довести, що є залежність між хаотичною поведінкою та великими й довготривалими змінами.

У вересні 2020 року до них приєднався Ендрю Кларк, аспірант, який навчався під керівництвом Гардії, і вони вирішили спробувати розв’язати проблему ще раз, цього разу включивши в модель додаткову планету. У їхній моделі три планети обертаються навколо Сонця на все більшій відстані одна від одної. Важливо, що найвіддаленіша планета починає обертатися під значним нахилом відносно другої та третьої планет, так що її орбіта утворює практично прямий кут з орбітами інших планет.

Цей нахил дозволив математикам знайти початкові умови, які призводять до нестабільності.

Вони виявили траєкторії, які могли призвести до виникнення практично будь-якого можливого ексцентриситету для другої планети: З часом її еліпс міг сплющитися, поки не став майже схожим на пряму лінію. Водночас орбіти другої та третьої планет, які починалися в одній площині, також могли стати перпендикулярними одна до одної. Друга планета могла навіть розвернутися на цілих 180 градусів, тож якщо спочатку всі планети рухалися навколо Сонця за годинниковою стрілкою, то друга – проти годинникової стрілки. «Уявіть, що ви зазирнете на мільйон років вперед, а Марс рухається в протилежний бік», – каже Річард Монтгомері з Каліфорнійського університету в Санта-Крузі. «Це було б дивно».

«Неможливо запобігти появі дуже химерних орбіт, навіть у цій простій моделі», – говорить Нідерман.

Попри це, розміри орбіт залишалися стабільними. Все тому, що в цій моделі планети рухаються навколо Сонця дуже швидко порівняно з тим, скільки часу потрібно для прецесії їхніх орбіт, що дозволяє математикам не брати до уваги «швидкі» змінні, пов’язані з рухом планет. «Аналізувати зміни рік за роком – це втомлює, якщо вас цікавить те, що відбудеться через тисячу років», – каже Мокель. Коливання розміру кожного еліпса вирівнюються (вимірювалися зміни довгого радіуса або великої осі).

Це не було несподіванкою. «Загальновідомо, що нахил і ексцентриситет повинні бути більш нестабільними, ніж велика піввісь», – каже Гардія. Але потім він і його колеги зрозуміли, що якщо вони розмістять третю планету ще далі від Сонця, то, можливо, зможуть збільшити нестабільність у своїй моделі.

Ця нова система і рівняння, які нею керували, були складнішими, і математики не були впевнені, що зможуть отримати якісь результати. Але «попередні результати були занадто красномовні, щоб їх ігнорувати», – каже Кларк. «Якщо був шанс показати, що півосі можуть зміщуватися, тоді треба це перевірити.»

Ласкар, який керував більшою частиною досліджень нестабільності Сонячної системи, сказав, що якщо накласти таку Сонячну систему на нашу власну, то можна було б побачити першу планету, розташовану впритул до Сонця, другу планету там, де була б Земля, і третю планету далеко за межами Хмари Оорта, на зовнішніх кордонах нашої Сонячної системи.  В результаті, додав він, це створює «дуже екстраординарну картину» – таку, яку він не обов’язково очікує зустріти в нашій галактиці.

Чим більша відстань планети від Сонця, тим більше часу їй потрібно для проходження орбіти. У цій моделі третя планета знаходиться настільки далеко, що прецесія двох внутрішніх планет відбувається з більшою швидкістю. Усереднювати рух останньої планети вже неможливо – сценарій, який Лагранж і Лаплас не врахували у своїх розрахунках стабільності Сонячної системи. «Це повністю змінить структуру рівняння», – переконаний Ален Шенсінер, математик з Паризької обсерваторії. Відтепер було більше змінних, про які слід подбати.

Кларк, Фехос і Гардія довели, що орбіти можуть збільшуватися як завгодно. «Вони нарешті отримали збільшення розміру орбіти, а не лише її форми чи чогось подібного», – сказав Мокель. «Це і є абсолютна нестабільність».

Попри те, що ці зміни накопичувалися дуже повільно, вони все ж відбулися швидше, ніж можна було очікувати – це свідчить про те, що в реальній планетній системі зміни можуть накопичуватися протягом сотень мільйонів, а не мільярдів років.

Результати дослідження дають теоретичне пояснення того, чому планети нашої Сонячної системи мають орбіти, які лежать майже в одній площині. Вони показують, що така проста річ, як великий кут нахилу, може стати джерелом значної нестабільності, причому з кількох причин. «Якщо ви почнете з ситуації, коли взаємні нахили досить великі, то ви зруйнуєте всю систему досить «швидко», – каже Ченсінер. «Вона ламається на сотні або тисячі століть швидше».

Багатовимірні магістралі

Ці докази вимагали розумного поєднання методів геометрії, аналізу та динаміки – і повернення до базових понять.

Математики представили кожну конфігурацію своєї планетної системи (положення і швидкості планет) як точку у багатовимірному просторі. Їхньою метою було показати існування «магістралей» у просторі, які відповідають, скажімо, великим змінам в ексцентриситеті другої планети або в півосі третьої планети.

Для цього їм спочатку довелося виразити кожну точку в термінах координат, які були настільки езотеричними й складними, що навряд чи хтось навіть чув про них, не кажучи вже про те, щоб спробувати їх використати. Координати були відкриті на початку 1980-х років бельгійським астрономом Андре Депрі, потім забуті, а згодом незалежно повторно відкриті Пінзарі у 2009 році, коли вона працювала над своєю докторською дисертацією.  Відтоді їх майже не використовували.

Використовуючи координати Депріта для опису свого багатовимірного простору планетарних конфігурацій, математики отримали глибше розуміння його структури. «У цьому полягає частина краси доведення: впоратися з цією 18-вимірною геометрією», – сказав Фейхоз.

Фехос, Кларк і Гардія знайшли магістралі, які перетинали кілька особливих регіонів у цьому просторі. Потім вони використали своє нове геометричне осмислення, щоб довести, що ці магістралі відповідають нестабільній динаміці розміру та форми орбіт планет.

«Коли я закінчив свою докторську дисертацію 30 років тому, – згадує Нідерман, – ми були дуже, дуже далекі від таких результатів».

«Це настільки складна система, що виникає відчуття, ніби все, що не є очевидно забороненим, має відбуватися», – сказав Ченсінер. «Але зазвичай всі події в ній доволі складно довести».

Тепер математики сподіваються використати методи Кларка, Фейхоса і Гардіа для доведення нестабільності в моделях, які більше схожі на нашу власну Сонячну систему. Такі результати набувають особливого значення, оскільки астрономи відкривають все більше і більше екзопланет, що обертаються навколо інших зірок, демонструючи широкий спектр конфігурацій. »Це схоже на відкриту лабораторію», – каже Маріан Гідеа, математик з Приватного університету Нью-Йорка. «Бачити на папері, які типи еволюції планетних систем можуть відбуватися, і порівнювати це з тим, що ти можеш спостерігати – це надзвичайне відчуття. Там ми багато дізнаємося про фізику нашого Всесвіту і про те, як багато з цього наша математика здатна вловити за допомогою відносно простих моделей».

В надії зробити таке порівняння, Фехос розмовляв з кількома астрономами про виявлення позасонячних систем, які хоча б віддалено нагадують модель, розроблену ним і його колегами. Інші дослідники, в тому числі Гідеа, кажуть, що робота може стати в пригоді для розробки ефективних траєкторій для штучних супутників або для з’ясування того, як переміщувати частинки на високих швидкостях за допомогою прискорювача частинок. Як сказала Пінзарі, «дослідження в галузі небесної механіки все ще дуже активні».

Кінцевою метою науковців є доведення нестабільності нашої власної Сонячної системи. «Я прокидаюся посеред ночі, думаючи про це», – поділився Кларк. «Я б сказав, що це був сон наяву, але це міг би бути й кошмар, чи не так? Тому що нічим хорошим це б не скінчилося».

Уточнення: 16 травня 2023 року У цю статтю було внесено зміни, адже Марсель Гардія є професором Барселонського університету. Він перейшов з Політехнічного університету Каталонії влітку 2022 року.

Джерело